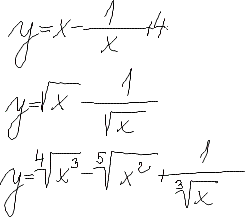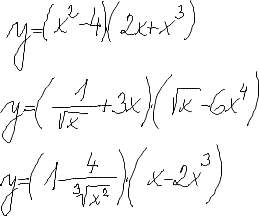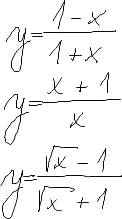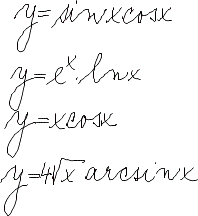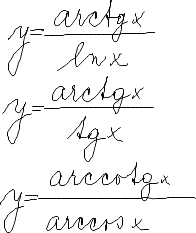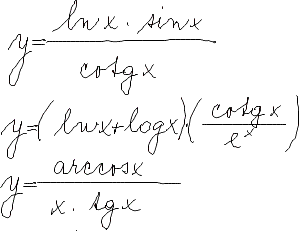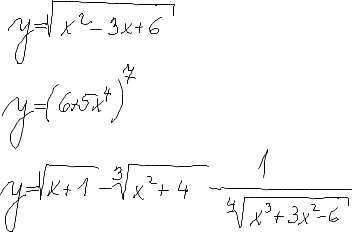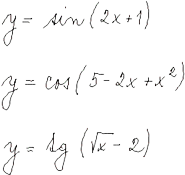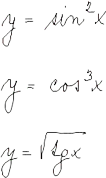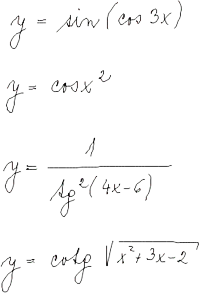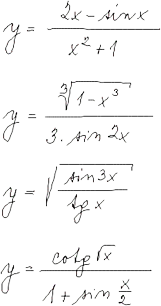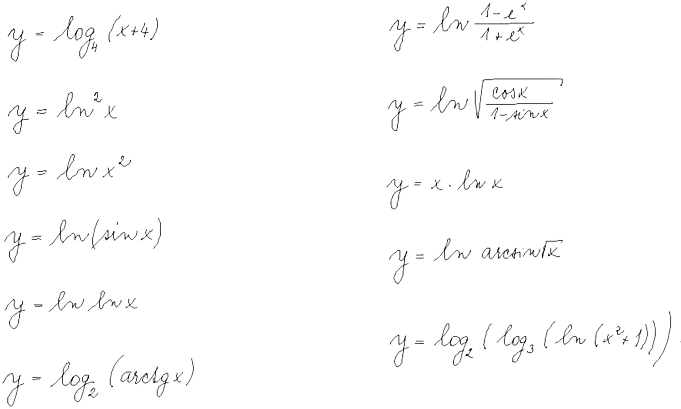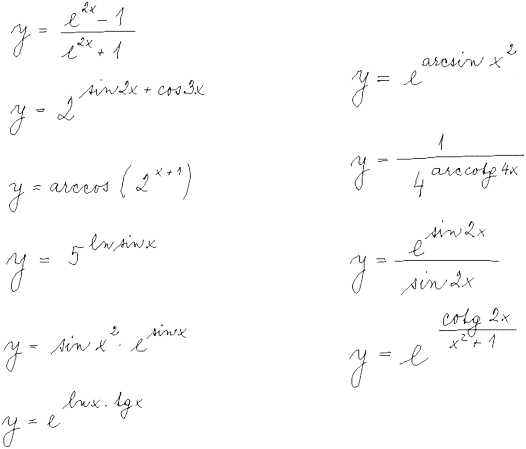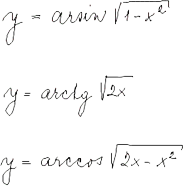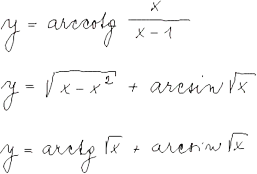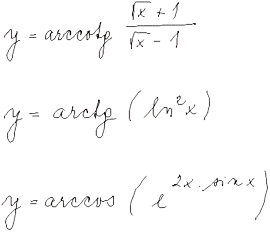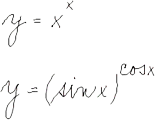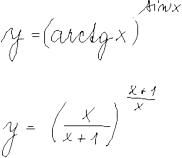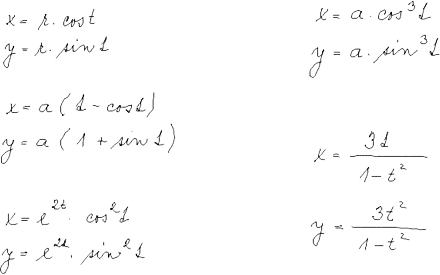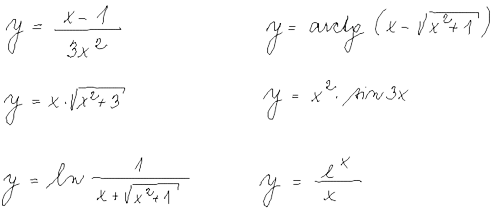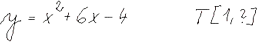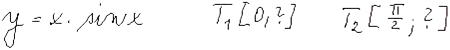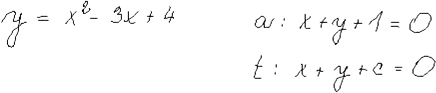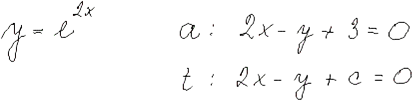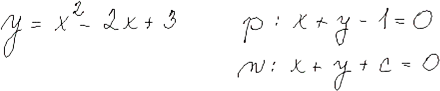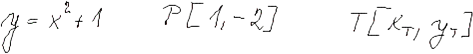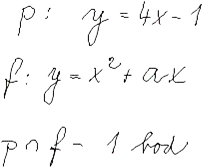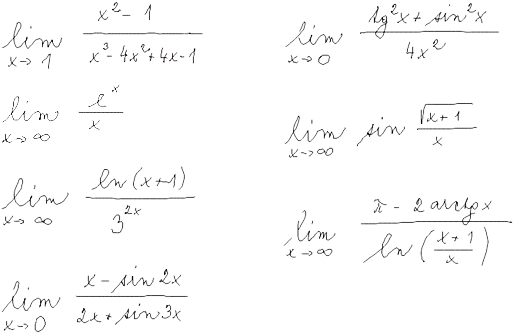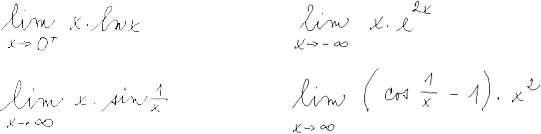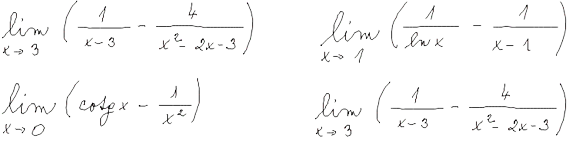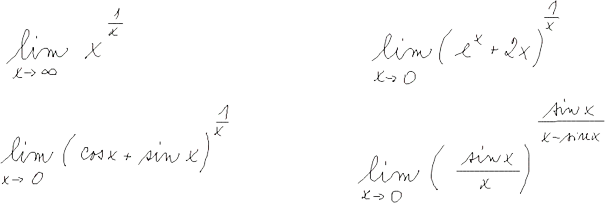Diferenciální počet funkcí jedné proměnné
Skripta (Plná verze k tisku)
Burda, P., Havelek, R., Hradecká, R., Kreml, P.: Matematika I (2006)
Dlouhá, D., Hamříková, R., Morávková, Z., Tužilová, M.: Matematika I: Pracovní listy (2014)
Hamříková, R.: Sbírka úloh z matematiky (2007)
Morávková, Z., Schreiberová, P.: Studijní karta s přehledem učiva (Derivace funkce a její aplikace)
Vybrané kapitoly skript Matematika I - Diferenciální počet funkcí jedné proměnné
Videa - Diferenciální počet funkce jedné proměnné
Derivace funkce
Derivace parametricky zadané funkce
Tečna a normála grafu funkce
Tečna a normálaTaylorův polynom
Taylorův polynom| Taylorův polynom |
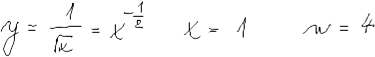 |
| Taylorův polynom |
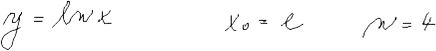 |
| Taylorův polynom |
 |
| Maclaurinův polynom |
 |
| Maclaurinův polynom |
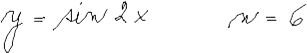 |
| Maclaurinův polynom |
 |
| Maclaurinův polynom |
 |
| Maclaurinův polynom |
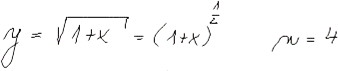 |
| Maclaurinův polynom |
 |
L'Hospitalovo pravidlo
Průběh funkce
Průběh funkce (část 1)Průběh funkce (část 2)
| Absolutní (globální) extrémy funkce |
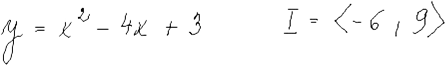 |
| Absolutní (globální) extrémy funkce |
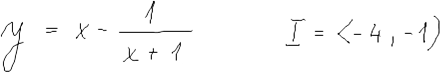 |
| Absolutní (globální) extrémy funkce |
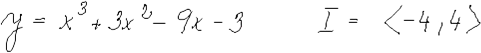 |
| Průběh funkce |
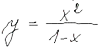 |
| Průběh funkce |
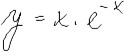 |
| Průběh funkce |
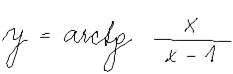 |
| Průběh funkce |
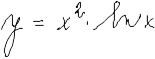 |
| Průběh funkce |
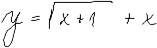 |
| Průběh funkce |
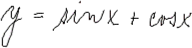 |